Peak fitting

There are four peak fitting options:

• Gaussian
• Lorentzian
• Voigt
• Resonance

With the exception of the single Resonance peak option, each of these offer a maximum of 10 peaks to fit the data. The initial estimate of the positions of each peak is picked using the “pick peaks” cursor tool found in the Context Menu. 

When you have fitted a peak, the right hand pane will show the fitting coefficients in terms of the amplitude a, the width w, the peak position p and any constant offset c. The amplitude value will be with respect to this offset. The width approximates to the full width half maximum of the peak (again with respect to any offset) and the position is the centre of the peak.

The peak types.

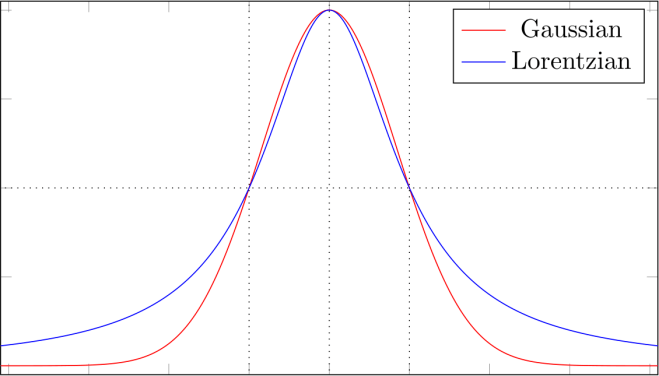
Above we have a comparison of a Gaussian and a Lorentzian profile, scaled to have the same height and width.

The Voigt profile is simply a linear combination** of these two, where the ratio of their contributions can be adjusted by a value of 0.1 to 0.9. When you have selected the Voigt option and chosen the number of peaks to fit, you will be prompted to modify the Voigt ratio, or keep the current value. A setting of 0.1 is nearly pure Lorentzian and 0.9 nearly pure Gaussian, with the default of 0.5 being an equal contribution from each.

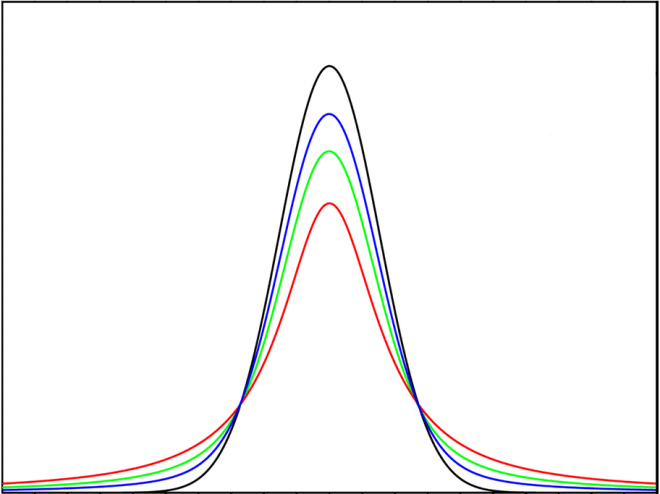
This plot shows a series of Voigt profiles from Gaussian to Lorentzian.

Why use these particular peaks? Because these shapes occur quite commonly in nature. For example, take a spectral line such as the emission of a laser beam. Whilst you might expect a perfect laser to have only one emission frequency, and therefore be a narrow line, in practice the narrow line is broadened in frequency by physical processes. Doppler broadening gives a Gaussian profile, whilst collision broadening (sometimes called pressure broadening) and lifetime broadening give a Lorentzian profile. Spectral lines of many different origins (lasers, atomic transitions etc.) often exhibit shapes that are broadened by some combination of these processes.

The Resonance peak option is designed to fit damped, driven harmonic oscillator data that you might find in mechanical or electrical systems. Damped resonance curves are not symmetrical and CFTool fits assuming the typical asymmetry of a mechanical system.

Peak fitting tips.

CFTool offers you the possibility of fitting up to 10 peaks on a graph simultaneously. However, this means that all of the peaks will have a common baseline. If this is true for your data then fine, but if your peaks are superimposed on a changing baseline, you may find it easier to fit one or two peaks close together and place the fitting limits just outside the peaks. The plot below only required two peaks to make this fit. 

There is a trick that allows you to deal with changing baselines by choosing some “peaks” on the line between the main peaks to adapt the curve to the baseline. This can work well, but means you have to be very careful as to which set of coefficients correspond to the main peaks of interest. The plot below uses this technique, but required all 10 peaks to define the shape.

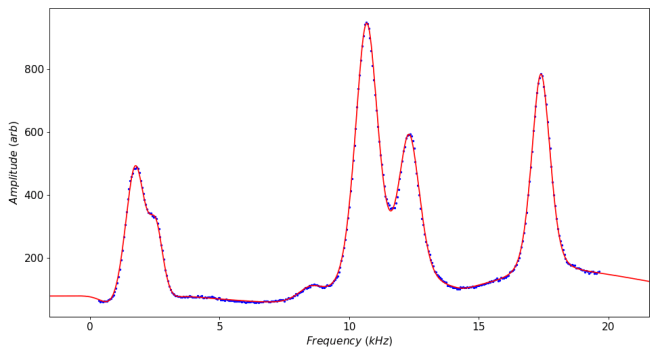
** The linear combination used in CFTool should more strictly be called a pseudo-Voigt as the pure Voigt function is a convolution of a Lorentzian and a Gaussian. However, the pseudo-voigt is more commonly used in peak fitting and is often the better choice.